I cd = moment of inertia of the rectangular section about the cd line the next step involves determining the value or expression for the moment of inertia of the rectangular plate about the line cd. here we will take one ixy moment of inertia rectangle rectangular elementary strip with a thickness dy that will be at a distance y from the line cd. To get the ixy The first method.
The product of inertia of area a relative to the indicated ixy moment of inertia rectangle xy rectangular axes is ixy = ∫ xy da. the product of inertia of the mass contained in volume v relative to the xy axes is ixy = ∫ xyρ dv—similarly for iyz and izx. Moment of inertia and properties of plane areas the moment of inertia (i) is a term used to describe the capacity of a cross-section to resist bending. it is always considered with respect to a reference axis such as x-x or y-y. it is a mathematical property of a section concerned with a surface area and how. May 02, 2020 · the moment of inertia of a rectangle with respect to a centroidal axis perpendicular to its base, can be found, by alternating dimensions b and h, in the first equation above: i_y = \frac{h b^3}{12}-\frac{h_{h} b_{h}^3}{12}.
Where ix, iy the moments of inertia about the initial axes and ixy the product of inertia. iu, iv and iuv are the respective quantities for the rotated axes u,v. the product of inertia ixy of a rectangular tube, about centroidal x,y axes, is zero, because x and y are also symmetry axes. Moment of inertia for instance, if you're looking how to calculate the moment of inertia of a rectangle you can use the tool above simply by selecting rectangle from the drop down list then entering some dimensions for height and width (e. g. 100, 200). after clicking "calculate", the tool will calculate the moment of inertia.
What Is The Product Of Inertia Quora
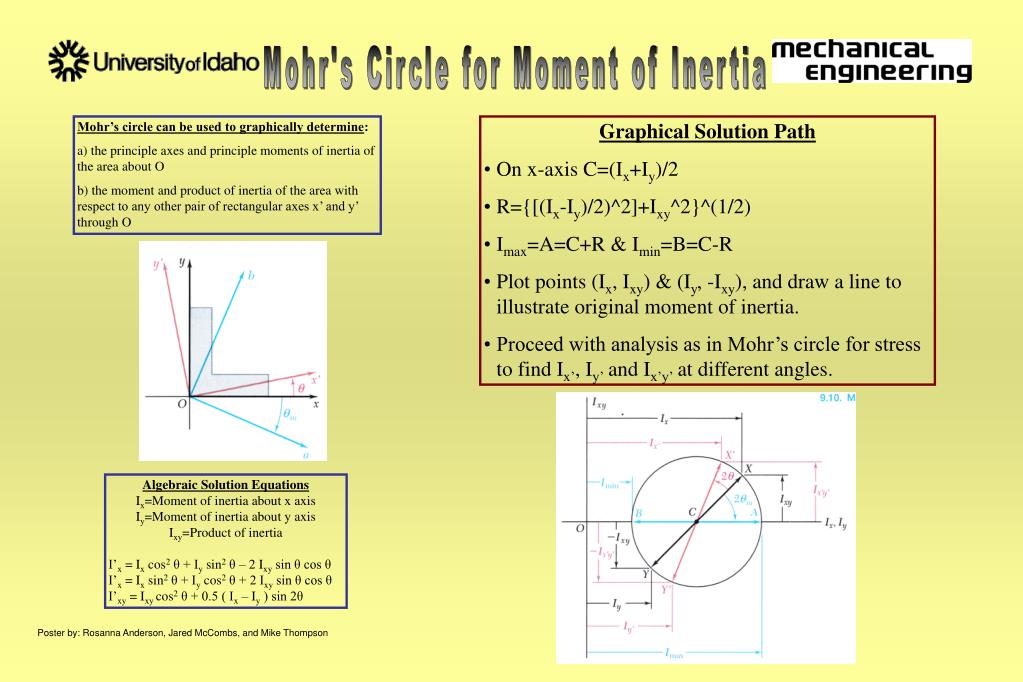
More ixy moment of inertia rectangle images. Analytically determine the moments and product of inertia for any other rectangular axes including the principal axes and principal moments and products of inertia. 10. 8 mohr’s circle for moments and products of inertia sample problem 10. 7 9 11 for the section shown, the moments of inertia with respect to the xand yaxes are ix= 10. 38 in 4 and i. When we take a situation when the axis passes through the centroid, the moment of inertia of a rectangle is given as: i = bh 3 / 12. here, b is used to denote the rectangle width (the dimension parallel to the axis) and h is said to be the height (dimension perpendicular to the axis). 2. an axis passing through its base. The moment of inertia, for the rectangular section at the y-axis passing by the external axis at the left corner, by using the infinitesimal area (dx*dy), we ixy moment of inertia rectangle will use a double integration method. 1-the strip area =dx*dy, and the horizontal distance from the cg of that strip to the vertical axisy=x.
When we take a situation when the axis passes through the centroid, the moment of inertia of a rectangle is given as: i = bh 3 / 12 here, b is used to denote the rectangle width (the dimension parallel to the axis) and h is said to be the height (dimension perpendicular to the axis). 2. Apply the parallel axis theorem to each rectangle, ixy =∑(ixy′ ′+ xya) note that the product of inertia with respect to ixy moment of inertia rectangle centroidal axes parallel to the xy axes is zero for each rectangle. ixy =∑ xya =− 6. 56 in4 3/31/2014 5. Find area moment of inertia. search a wide range of information from across the web with allinfosearch. com. Finding product of inertia example 10 determine the moment of inertia and the product of inertia of a wooden t-beam section. each leg is comprised of a 2 x 10. the centroid is 8” above the base. the centroidal moments of inertia and the product of inertia are determined using the table below product of inertia = ixy = a (dx)(dy) = 0 8” 3”-3”.
5product Of Inertia Ixy Ip For The Rectangular Section
Help Moment Of Inertia Ixx Iyy Izz Ixy Ixz Iyz Etc

Moment of inertia 5 an example of this is the concrete t-beam shown. although it is a simple matter to determine the moment of inertia of each rectangular section that makes up the beam, they will not reference the same axis, thus cannot be added. however, if we found the moment of inertia of each section about some. Order today with free shipping. get the deals now!. To get the ixy at the cg for a rectangle, we consider the moment of inertia about the two axes passing by the cg. 1the rectangle can be considered as composed of 4 equal areas, like quarters, each quarter =a/4, for the first quarter the x distance is at the left of y’ axis, so the x distance is =-b/4, while the y 1 is =h/4 with a positive sign.
Given the moment of inertia of a rectangle about its centroidal axis, apply the parallel axis theorem to find the moment of inertia for a rectangle about its base. examples for moment of inertia 8 b h c xc yc x ixc = b⋅h3 12 distance = h 2 area = b⋅h ix = b⋅h3 12 h 2 2 ⋅ b⋅h = b⋅h3 12 b⋅h3 4 = b⋅h3 12 3⋅b⋅h3 12 = b⋅h3 3. The moment of inertia of a rectangular tube with respect to an axis passing through its centroid, is given by the following expression: where, b is the tube total width, and specifically its dimension parallel to the axis, and h is the height (more specifically, the dimension perpendicular to the axis) and t is the thickness of the walls.
Ixy And Principal Axis Ppt Islamic University Of Gaza
For instance, if you're looking how to calculate the moment of inertia of a rectangle you can use the tool above simply by selecting rectangle from the drop down list then entering some dimensions for height and width (e. g. 100, 200). after clicking "calculate", the tool will calculate the moment of inertia. our paid version will show the full hand calculations of how the tool got to this. Looking for moment of inertia rectangle? search now! content updated daily for moment of inertia rectangle. Finding product of inertia example 10 determine the moment of inertia and the product of inertia of a wooden t-beam section. each leg is comprised of a 2 x ixy moment of inertia rectangle 10. the centroid is 8” above the base. the centroidal moments of inertia and the product of inertia are determined using the table below product of inertia = ixy = a (dx)(dy) = 0 8” 3.
The moment of inertia of a rectangle with respect to an axis passing through its centroid, is given by the following expression: where b is the rectangle width, and specifically its dimension parallel to the axis, and h is the height (more specifically, the dimension perpendicular to the axis). The moment of inertia is also known as the second moment of the area and is expressed mathematically as: i x = ∫ ay 2da i y = ∫ ax 2da where y = distance from the x axis to area da x = distance from the y axis to area da example radius of gyration: x x i k a = y y i k a =.
0 Response to "Ixy Moment Of Inertia Rectangle"
Post a Comment